En mathématiques l’ellipse fait partie de la conique. On trouve trois sortes de courbe appartenant à la conique : le cercle, l’ellipse et l’hyperbole. L’orbite circulaire a une excentricité ( e ) nulle, pour l’elliptique 0<e<1 et e>1 pour l’hyperbolique. Nous allons nous focaliser sur l’ellipse. Nous savons que lorsque que l’on lance un satellite, selon l’énergie fournie au satellite, celui-ci peut soit se trouver en état de diffusion et sa trajectoire forme alors une hyperbole, soit se placer en orbite, on dit qu’il est dans un état lié, il forme alors une ellipse. Cependant, afin de se placer sur une orbite, il faut que le satellite décrive une ellipse:
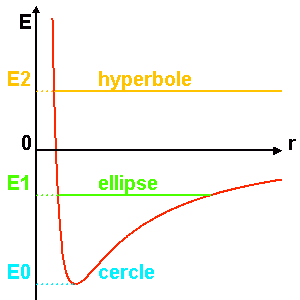
Selon l'énergie mécanique insuflée, le satellite peut décrire différents types de trajectoires
Ainsi le satellite va décrire une orbite correspondant au schéma suivant :
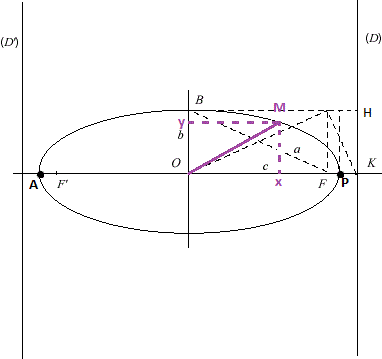
L’orbite elliptique se caractérise par un foyer (F), une apogée (AF) et un périgée (FP). La Terre correspond au foyer. De plus, l’orbite se caractérise aussi par le demi grand axe noté a et le demi petit axe noté b. Les axes 2a et 2b forment un repère orthonormé de centre O (O ne correspondant pas à la Terre). Nous savons aussi grâce à certains calculs que BF=a. En effet, l’ellipse est aussi caractérisée par une droite directrice (D) et pour un point M(x ; y) de l’ellipse on a (selon la définition d’une ellipse) MF=e*MH avec H un point de la directrice tel que MH soit parallèle à AP (AP=2a).
Nous avons l’équation de l’ellipse en mathématique : (x²/a²) + (y²/b²) = 1
Nous allons chercher à determiner l'équation de l'orbite elliptique pour un type d'orbite en particulier : L'orbite de Molniya. C'est une orbite très elliptique d'apogée 40000km et de périgée 1000km.
On a :
- OP = a
- OF = a - FP ⇔ OF = c
- BFO triangle rectangle en O
- a est l'hypoténuse et b et c les deux autres côtés
- c = a - FP
On va donc utiliser le théorème de Pythagore pour cette équation. Selon le théorème de Pythagore, a² = c² + b²
On a AP = AF + FP ⇔ AP = 41000. De plus AP = 2a. Donc a = 41000/2 = 20500
De plus on a : c = a -FP ⇔ c = 20500-1000
⇔ c = 19500
On peut donc dire que :
b = racine carrée (a² - c²) ⇔ b = racine carrée (20500² - 19500²)
⇔ b = racine carrée (40000000)
⇔ b = 6324,55532
Ainsi, l'équation de l'orbite elliptique de Molniya est, pour tout point M (x ; y) de l'orbite :
( x² / 20500² ) + ( y² / 6324,55532² ) = 1
